We can see that the graph touches
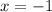 without crossing the x-axis (i.e. it is a double solution), and then there's another zero at
without crossing the x-axis (i.e. it is a double solution), and then there's another zero at
 (this time it's a crossing zero, so a single solution).
(this time it's a crossing zero, so a single solution).
This leads, up to multiple, to the polynomial
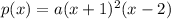
If we impose the passing through
 we have
we have

So, the polynomial is

Finally, to solve
 , simply look at the graph, searching for the points, where the graph is below the x-axis. You can see that this happens only if
, simply look at the graph, searching for the points, where the graph is below the x-axis. You can see that this happens only if
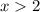 , so that's the solution to your question.
, so that's the solution to your question.