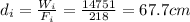Question

25. A student is removing rocks from a garden. She exerts a force of 218 N on a lever to raise one rock a distance of 11.0 cm.

a. If the rock weighs 1050 N, how far does the girl move her end of the lever if the lever is an ideal machine?
b. If the lever actually has an efficiency of 78.3 percent, how far does the girl move her end of the lever?

Answer 1

a) 53.0 cm

b) 67.7 cm

Step-by-step explanation:

a)

In an ideal lever (100% efficiency), the work done in input is equal to the work done in output. So we can write:

`W_(in) = W_(out)`

And both works can be rewritten as

`F_i d_i = F_o d_o`

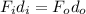
where

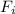`F_i` is the force in input

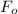`F_o` is the force in output

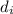`d_i` is the effort arm

`d_o` is the load arm

Here we have:

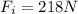`F_i=218 N` is the force exerted in input

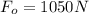`F_o=1050 N` is the output force (the weight of the rock)

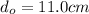`d_o = 11.0 cm` is the distance through which the rock is lifted

So, we can find the distance through which the lever moves on the input end:

`d_i = (F_o d_o)/(F_i)=((1050)(11.0))/(218)=53.0 cm`

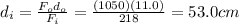
b)

In this case, the lever has an efficiency of

`\eta = 78.3\% = 0.783`

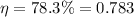
Efficiency can be rewritten as the ratio between output work and input work:

`\eta=(W_o)/(W_i)`

The output work is

`W_o=F_o d_o =(1050)(11)=11,550 N\cdot cm`

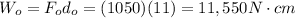
Therefore the input work is

`W_i = (W_o)/(\eta)=(11550)/(0.783)=14,751 N\cdot cm`

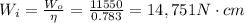
This input work can be rewritten as

`W_i = F_i d_i`

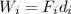
And so we can find by how much the girl moves her end of the lever in this case:

`d_i=(W_i)/(F_i)=(14751)/(218)=67.7 cm`