Answer:
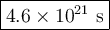
Step-by-step explanation:
Whenever a question asks you, "What is the concentration after a given time?" or something like that, you must use the appropriate integrated rate law expression.
The reaction is 2nd order, because the units of k are L·mol⁻¹s⁻¹.
The integrated rate law for a second-order reaction is
![\frac{1}{\text{[A]}} =\frac{1}{\text{[A]}_(0)}+ kt](https://img.qammunity.org/2021/formulas/chemistry/middle-school/n6vy4xgi8rjci25080jfi88d3z339ga4d5.png)
Data:
k = 2.4 × 10⁻²¹ L·mol⁻¹s⁻¹
[A]₀ = 0.0100 mol·L⁻¹
[A] = 0.009 00 mol·L⁻¹
Calculation :
![\begin{array}{rcl}\frac{1}{\text{[A]}} & = & \frac{1}{\text{[A]}_(0)}+ kt\\\\(1)/(0.00900 )& = & (1)/(0.0100) + 2.4 * 10^(-21) \, t\\\\111.1&=& 100.0 + 2.4 * 10^(-21) \, t\\\\11.1& = & 2.4 * 10^(-21) \, t\\t & = & (11.1)/( 2.4 * 10^(-21))\\\\& = & \mathbf{4.6 * 10^(21)}\textbf{ s}\\\end{array}\\\text{It will take $\large \boxed{\mathbf{4.6 * 10^(21)}\textbf{ s}}$ for the HI to decompose}](https://img.qammunity.org/2021/formulas/chemistry/middle-school/4hc2izelf0886st540g6ou0nmcbffh96tr.png)