Question

At 25 oC, hydrogen iodide breaks down very slowly to hydrogen gas and iodine vapor with a rate constant of 2.4 x 10-21L/mol.s. If 0.0100 mol of HI(g) is placed into a 1.0 L container at 25 oC, how long will it take for the concentration of HI to reach 0.00900 mol/L?

Answer 1

`\large \boxed{4.6 * 10^(21)\text{ s}}`

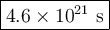
Step-by-step explanation:

Whenever a question asks you, "What is the concentration after a given time?" or something like that, you must use the appropriate integrated rate law expression.

The reaction is 2nd order, because the units of k are L·mol⁻¹s⁻¹.

The integrated rate law for a second-order reaction is

`\frac{1}{\text{[A]}} =\frac{1}{\text{[A]}_(0)}+ kt`

Data:

k = 2.4 × 10⁻²¹ L·mol⁻¹s⁻¹

[A]₀ = 0.0100 mol·L⁻¹

[A] = 0.009 00 mol·L⁻¹

Calculation :

`\begin{array}{rcl}\frac{1}{\text{[A]}} & = & \frac{1}{\text{[A]}_(0)}+ kt\\\\(1)/(0.00900 )& = & (1)/(0.0100) + 2.4 * 10^(-21) \, t\\\\111.1&=& 100.0 + 2.4 * 10^(-21) \, t\\\\11.1& = & 2.4 * 10^(-21) \, t\\t & = & (11.1)/( 2.4 * 10^(-21))\\\\& = & \mathbf{4.6 * 10^(21)}\textbf{ s}\\\end{array}\\\text{It will take $\large \boxed{\mathbf{4.6 * 10^(21)}\textbf{ s}}$ for the HI to decompose}`