Explanation:
Checking Option F:
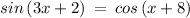
Checking x = 11° in above equation
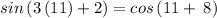
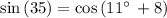
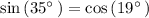
Checking x = 79° in above equation
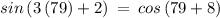
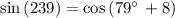
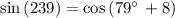
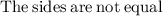
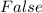
Checking Option G:
Checking x = 20° in above equation
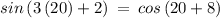
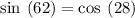
The sides are not equal
False
Checking x = 70° in above equation
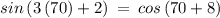
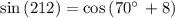
The sides are not equal
False
Checking Option H:
Checking x = 44° in above equation
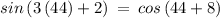
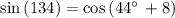
The sides are not equal
False
Checking x = 46° in above equation
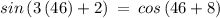
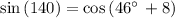
The sides are not equal
False
Checking Option J:
Checking x = 62° in above equation
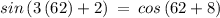
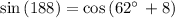
The sides are not equal
False
Checking x = 28° in above equation
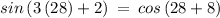
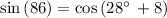
The sides are not equal
False
Therefore, NO TWO angles satisfy the equation
sin(3x + 2) = cos(x + 8).