Question

A quantity b varies jointly with c and d and inversely with eWhen b is 18, c is 4, d is 9, and e is 6What is the constant of variation?

Answer 1

`b=(3cd)/(e)`

Explanation:

b ∝ c d*
`(1)/(e)`

`b=(kcd)/(e)`

Now substitute the values to find k

`18=(k*4*9)/(6) \\36k=108\\k=(108)/(36) \\k=3`

The relationship will be:

`b=(kcd)/(e)\\b=(3cd)/(e)`

Answer 2

constant of variation = 3

Explanation:

we know that b varies jointly with c and d

so:

b∝c∝d

and b varies inversely with e, so

b∝
`(1)/(e)`

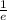
and i will call the constant of variation k, this way we can make an equation for b in the following form:

`b=k(cd)/(e)`

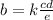
this satisfy that b varies jointly with c and d (if b increases, c and d also increase) and inversely with e (if b increases, e decreases)

we know that when b is 18, c is 4, d is 9, and e is 6:

`b=18\\c=4\\d=9\\e=6`

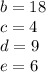
substituting this in our equation for b:

`b=k(cd)/(e)\\ 18=k((4)(9))/(6)`

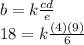
and we solve operations and clear for the constant of variation k:

`18=k(36)/(6)\\ 18=6k\\(18)/(6)=k\\ 3=k`

the constant of variation is 3.