Answer:
constant of variation = 3
Explanation:
we know that b varies jointly with c and d
so:
b∝c∝d
and b varies inversely with e, so
b∝
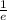
and i will call the constant of variation k, this way we can make an equation for b in the following form:
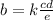
this satisfy that b varies jointly with c and d (if b increases, c and d also increase) and inversely with e (if b increases, e decreases)
we know that when b is 18, c is 4, d is 9, and e is 6:
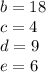
substituting this in our equation for b:
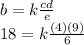
and we solve operations and clear for the constant of variation k:
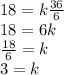
the constant of variation is 3.