Question

A bucket that weighs 6 lb and a rope of negligible weight are used to draw water from a well that is 50 ft deep. The bucket is filled with 40 lb of water and is pulled up at a rate of 2 ft/s, but water leaks out of a hole in the bucket at a rate of 0.2 lb/s. Find the work done in pulling the bucket to the top of the well.

Answer 1

Total work done =
`W_(water)+ W_(bucket)`

=
`1875+300 = 2175ft-lb.`

Explanation:

According to given scenario, there are two things being pulled to the top of the well.

1. Bucket

2. Water

So, we have to find work done separately for water and bucket.

For total work done, we have to add work done by water and work done by bucket.

Now, For the bucket,

The weight of the bucket is a constant 6 lb, and we"ll move the bucket a small distance Δ
`y`. We have these small distances from
`y = 0` to
`y = 50`.

`W_(bucket)` =
`\int\limits^(50)_0 {6} \, dy`

=
`(6* 50 - 6*0)`

=
`300`

Thus, the work to lift the bucket out of the well is
`300ft`
`-lb`.

For the water,

Water leak out of the bucket at a constant rate 0.2
`(lb)/(s)`, so the weight of the water can be modeled with a linear function.

Since well is
`50ft` deep, it takes

`(50ft)`
`((1s))/((2ft))` =
`25s`

to pull the bucket to top of the well after
`25s`, we lost,

`((0.2lb))/((1s)) * 25s` =
`5lb`

so,
`35lb` water remains in bucket.

Now, when
`y=0,` weight = 35 and when
`y=50`, weight = 40

Slope =
`((40-35))/((50-0))`

=
`(1)/(10)`

So, linear equation is

Weight =
`(1y)/(10) + b`

substituting the value,

`35 = (1*0)/(10) +b`

`b=35`

Now, the equation of water at any depth y in the well is written as.

`(1* y)/(10) +35`

if we move small distance Δ
`y`, we have distances from
`y=0` to
`y=50`

`W_(water)` =
`\int\limits^(50)_(0) {(1* y)/(10)+35 } \, dy`

=
`((50^(2) )/(2)* (1)/(10)+35* 50) -((1)/(10)* (0^(2) )/(2)+35* 0)`

=
`(125+1750) - (0+0)`

=
`1875`

Now,

Total work done =
`W_(water)+ W_(bucket)`

=
`1875+300 = 2175ft-lb.`

Answer 2

Therefore total work done =2050 ft-lb

Explanation:

Given that, a bucket are used to drawn water from a well that is 50 ft deep.

(1)

Work done = Force×displacement.

Work done to pull the bucket is

= Weight of the bucket × displacement

=(6×50) ft-lb

=300 ft-lb

(2)

The bucket fill with 40 lb of water and is pulled up at a rate of 2ft/s, but leaks out of a hole in the bucket at a rate of 0.2 lb/s.

Since the well is 50 ft deep.

It takes
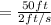`=(50ft)/(2ft/s)` =25 s to pull the bucket at the top of the well.

After 25 s it lost (25×0.2)lb =5 lb water.

So the remaining water is = (40-5) lb= 35 lb

Let y is distance above the original depth of 50 ft.

When y=50 ft, weight of the bucket= 40 lb,when y=0 weight of the bucket= 35 lb

The slope of the of water leakage is

`=(40-35)/(50-0)`

`=(1)/(10)`

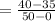
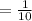
The bucket holds
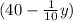`(40-\frac1{10}y)` lb of water when it is y ft above the original depth.

Work done to pull the water in the bucket is

`=\int _0^(50)(40-\frac1{10}y)dy`

`=[40y- \frac1{10}y^2]_0^(50)`

`=[(40* 50)-\frac1{10}(50)^2]-[(40* 0)-\frac1{10}(0)^2]`

=1750 ft-lb

Therefore total work done

=Work done to pull the bucket+Work done to pull the water in the bucket

=(300+1750) ft-lb

=2050 ft-lb