Answer:
Therefore total work done =2050 ft-lb
Explanation:
Given that, a bucket are used to drawn water from a well that is 50 ft deep.
(1)
Work done = Force×displacement.
Work done to pull the bucket is
= Weight of the bucket × displacement
=(6×50) ft-lb
=300 ft-lb
(2)
The bucket fill with 40 lb of water and is pulled up at a rate of 2ft/s, but leaks out of a hole in the bucket at a rate of 0.2 lb/s.
Since the well is 50 ft deep.
It takes
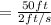 =25 s to pull the bucket at the top of the well.
=25 s to pull the bucket at the top of the well.
After 25 s it lost (25×0.2)lb =5 lb water.
So the remaining water is = (40-5) lb= 35 lb
Let y is distance above the original depth of 50 ft.
When y=50 ft, weight of the bucket= 40 lb,when y=0 weight of the bucket= 35 lb
The slope of the of water leakage is
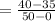
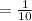
The bucket holds
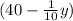 lb of water when it is y ft above the original depth.
lb of water when it is y ft above the original depth.
Work done to pull the water in the bucket is
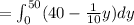
![=[40y- \frac1{10}y^2]_0^(50)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ek7q79km9n247tjuvpueudnbyfrlv7kdnu.png)
![=[(40* 50)-\frac1{10}(50)^2]-[(40* 0)-\frac1{10}(0)^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5f1xzlboe6f6qvue54sndm4mdg87u4qci2.png)
=1750 ft-lb
Therefore total work done
=Work done to pull the bucket+Work done to pull the water in the bucket
=(300+1750) ft-lb
=2050 ft-lb