Question

You have devised an experiment to measure the kinetic coefficient of friction between a ramp and block. You place the block on the ramp at an angle high enough that it starts sliding. You measure the time it takes to fall down a known distance. The time it takes to fall down the ramp starting from a standstill is 0.5 sec, ???? = 1 kg, θ = 45o, and the distance it falls, L, is 0.5 m. What is µk? (8 pts)

Answer 1

The μ = 0.422

Step-by-step explanation:

The distance travelled by the mass is equal to:

`L=ut+(1)/(2)at^(2) \\0.5=(0*5)+(1)/(2) a(0.5^(2) )\\a=4m/s^(2)`

The sum of forces in y-direction equals zero:

∑Fy = 0

N - (m * g * cosθ) = 0

N - (1 * 9.8 * cos45) = 0

N = 6.93 N

The sum of forces in x-direction is equal to:

∑Fx = ma

(m * g * sinθ) - fk = m * a

(1 * 9.8 * sin45) - fk = 1 * 4

fk = 2.93 N

fk = μ * N

2.93 = μ * 6.93

μ = 0.422

Answer 2

μ = 0.423

Step-by-step explanation:

To solve this exercise we must use Newton's second law and kinematics together, let's start using expressions of kinematics to find the acceleration of the body

Let's fix a reference system where the x axis is parallel to the inclined plane, but the acceleration is only on this axis

x = v₀ t + ½ a t²

The body starts from rest so its initial speed is zero

a = 2 x / t²

a = 2 0.5 /0.5²

a = 4 m / s²

Taking the acceleration of the body, we use Newton's second law, we take the direction up the plane as positive

X axis

fr - Wₓ = m a (1)

Y Axis

N-
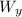`W_(y)` = 0

N = W_{y}

We use trigonometry to find the components of the weight

sin 45 = Wₓ / W

cos 45 = W_{y} / W

Wₓ = W sin 45

W_{y} = W cos 45

The out of touch has the expression

fr = μ N

fr = μ W_{y}

We substitute in 1

μ mg cos 45 - mg sin 45 = m a

W_{y} = (a + g sin 45) / g cos 45

μ = a / g cos 45 + 1

We calculate

Acceleration goes down the plane, so it is negative

a = -4 m / s²

μ = 1- 4 / (9.8 cos 45)

μ = 0.423