Question

Consider the statement: For all integers n, if n3 is even then n is even. a. Explicitly write out what you are supposing and what you are trying to prove, if you are proving the statement by proving the contrapositive. Suppose _______________________________________________________________________ Need to show ____________________________________________________________________ b. Prove the statement by the method of the contrapositive

Answer 1

It is proved that if
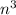`n^3` is even the n is even.

Explanation:

Given n is any integer.

To show
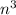`n^3` is even then n is even.

Proving by contrapositive suppose
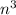`n^3` is odd. Then we need to show n is odd.

Then, letting k is a ny integer,

`n^3=2k+1\implies n=(2k+1)^{(1)/(3)}`

Now since (2k+1) is odd therefore n is odd.

Conversly let n is odd, then,

`n=2k+1\implies n^3=(2k+1)^3`

since 2k+1 is odd so
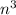`n^3` is odd.

This proves, if n is even then
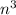`n^3` is even.