Answer:
P = $1664.12 pay with 9% compounded monthly
P = 1652.98 pay with 9% compounded continuously
Step-by-step explanation:
given data
time period = 20 year
amount = $10000
solution
we get here compound interest for 9% compounded monthly that is express as
FV =
 .................1
.................1
here P is principal amount and r is interest rate and n compound in year and FV is future value
$10000 =
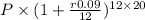
solve it we get
P = $1664.12 pay with 9% compounded monthly
and
for 9% compounded continuously
FV =
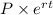 ............2
............2
$10000 = P\times e^{0.09\times 20}
solve it we get
P = 1652.98 pay with 9% compounded continuously