Question

A popular flashlight that uses two D-size batteries was selected, and several of the same models were purchased to test the "continuous-use life" of D batteries. As fresh batteries were installed, each flashlight was turned on and the time noted. When the flashlight no longer produced light, the time was again noted. The resulting "life" data from Rayovac batteries had a mean of 20.6 hours. Assume these values have a normal distribution with a standard deviation of 1.47 hours. (Give your answers correct to four decimal places.)

(a) What is the probability that one randomly selected Rayovac battery will have a test life between 20.4 and 22.2 hours?
(b) What is the probability that a randomly selected sample of 5 Rayovac batteries will have a mean test life between 20.4 and 22.2 hours?
(c) What is the probability that a randomly selected sample of 15 Rayovac batteries will have a mean test life between 20.4 and 22.2 hours?
(d) What is the probability that a randomly selected sample of 69 Rayovac batteries will have a mean test life between 20.4 and 22.2 hours?

Answer 1

(a) The probability that the randomly selected Rayovac battery will have a test life between 20.4 and 22.2 hours is 0.4178.

(b) The probability that the sample mean of 5 Rayovac battery will have a mean test life between 20.4 and 22.2 hours is 0.6104.

(c) The probability that the sample mean of 15 Rayovac battery will have a mean test life between 20.4 and 22.2 hours is 0.7019.

(d) The probability that the sample mean of 69 Rayovac battery will have a mean test life between 20.4 and 22.2 hours is 0.8708.

Explanation:

Let X = the life time of Rayovac batteries.

The lifetime of Rayovac batteries is Normally distributed with mean μ = 20.6 hours and standard deviation σ = 1.47 hours.

The standardized value of the sample mean of X is:

`z=(\bar X-\mu)/(\sigma/√(n))`

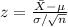
(a)

Compute the probability that the randomly selected Rayovac battery will have a test life between 20.4 and 22.2 hours as follows:

`P(20.4<X<22.2)=P((20.4-20.6)/(1.47)<(X-\mu)/(\sigma)<(22.2-20.6)/(1.47))`

`=P(-0.14<Z<1.09)\\=P(Z<1.09)-P(Z<-0.14)\\=0.8621-0.4443\\=0.4178`

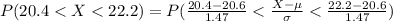
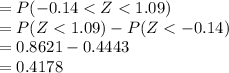
Thus, the probability that the randomly selected Rayovac battery will have a test life between 20.4 and 22.2 hours is 0.4178.

(b)

Compute the probability that the sample mean of 5 Rayovac battery will have a mean test life between 20.4 and 22.2 hours as follows:

`P(20.4<\bar X<22.2)=P((20.4-20.6)/(1.47/√(5))<(\bar X-\mu)/(\sigma/√(n))<(22.2-20.6)/(1.47/√(5)))`

`=P(-0.30<Z<2.43)\\=P(Z<2.43)-P(Z<-0.30)\\=0.9925-0.3821\\=0.6104`

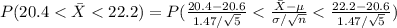
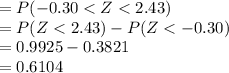
Thus, the probability that the sample mean of 5 Rayovac battery will have a mean test life between 20.4 and 22.2 hours is 0.6104.

(c)

Compute the probability that the sample mean of 15 Rayovac battery will have a mean test life between 20.4 and 22.2 hours as follows:

`P(20.4<\bar X<22.2)=P((20.4-20.6)/(1.47/√(15))<(\bar X-\mu)/(\sigma/√(n))<(22.2-20.6)/(1.47/√(15)))`

`=P(-0.53<Z<4.22)\\=P(Z<4.22)-P(Z<-0.53)\\=1-0.2981\\=0.7019`

Thus, the probability that the sample mean of 15 Rayovac battery will have a mean test life between 20.4 and 22.2 hours is 0.7019.

(d)

Compute the probability that the sample mean of 69 Rayovac battery will have a mean test life between 20.4 and 22.2 hours as follows:

`P(20.4<\bar X<22.2)=P((20.4-20.6)/(1.47/√(69))<(\bar X-\mu)/(\sigma/√(n))<(22.2-20.6)/(1.47/√(69)))`

`=P(-1.13<Z<9.04)\\=P(Z<9.04)-P(Z<-1.13)\\=1-0.1292\\=0.8708`

Thus, the probability that the sample mean of 69 Rayovac battery will have a mean test life between 20.4 and 22.2 hours is 0.8708.