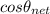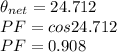Answer:
a)
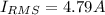
b)
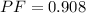
Step-by-step explanation:
Get the reactive powers for each of the loads:
Reactive power = Real Power * tanθ
For load 1
Active power, P₁ = 100 W
Power factor,
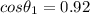
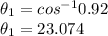
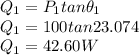
For load 2
Active power, P₂ = 250 W
Power factor,
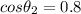
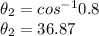
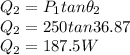
For load 3
Active power, P₃ = 250 W
Power factor,
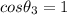
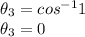
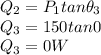
Calculate the total reactive power,
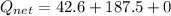

Calculate the total active power,
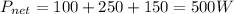
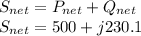
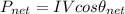
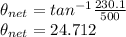
V = 115
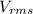
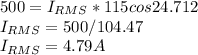
b) Power factor of the composite load is