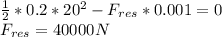Question

The design for a new cementless hip implant is to be studied using an instrumented implant and a fixed simulated femur.

Assuming the punch applies an average force of 2 kN over a time of 2 ms to the 200-g implant, determine (a) the velocity of the implant immediately after impact, (b) the average resistance of the implant to penetration if the implant moves 1 mm before coming to rest.

Answer 1

a) the velocity of the implant immediately after impact is 20 m/s

b) the average resistance of the implant is 40000 N

Step-by-step explanation:

a) The impulse momentum is:

mv1 + ∑Imp(1---->2) = mv2

According the exercise:

v1=0

∑Imp(1---->2) = F(t2-t1)

m=0.2 kg

Replacing:

`0+F(t_(2) -t_(1) )=0.2v_(2)`

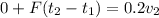
if F=2 kN and t2-t1=2x10^-3 s. Replacing

`0+2x10^(-3) (2x10^(-3) )=0.2v_(2) \\v_(2) =(4)/(0.2) =20m/s`

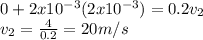
b) Work and energy in the system is:

T2 - U(2----->3) = T3

where T2 and T3 are the kinetic energy and U(2----->3) is the work.

`T_(2) =(1)/(2) mv_(2)^(2) \\T_(3) =0\\U_(2---3) =-F_(res) x`

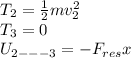
Replacing:

`(1)/(2) *0.2*20^(2) -F_(res) *0.001=0\\F_(res) =40000N`