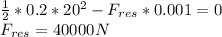Answer:
a) the velocity of the implant immediately after impact is 20 m/s
b) the average resistance of the implant is 40000 N
Step-by-step explanation:
a) The impulse momentum is:
mv1 + ∑Imp(1---->2) = mv2
According the exercise:
v1=0
∑Imp(1---->2) = F(t2-t1)
m=0.2 kg
Replacing:
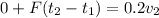
if F=2 kN and t2-t1=2x10^-3 s. Replacing
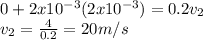
b) Work and energy in the system is:
T2 - U(2----->3) = T3
where T2 and T3 are the kinetic energy and U(2----->3) is the work.
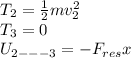
Replacing: