Answer:
The angular velocity of the coil is
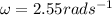 .
.
Step-by-step explanation:
The expression for the maximum emf is as follows;
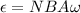 ......... (1)
......... (1)
Here,
 is the emf, {tex]\omega[/tex] is the angular velocity, N is the number of turns, B is the magnetic field and A is the area.
is the emf, {tex]\omega[/tex] is the angular velocity, N is the number of turns, B is the magnetic field and A is the area.
Calculate the area of the square coil.
Convert side of the length form cm to m.
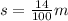
s= 0.14 m
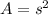
Here, A is the area and s is the length of the side of the square.
Put s= 0.14 m.
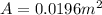
Convert maximum emf from mV to V.

Calculate the angular velocity of the coil by rearranging the equation (1).
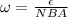
Put
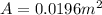 ,
,
 , B= 0.040 T and N= 18 turns.
, B= 0.040 T and N= 18 turns.
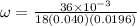
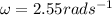
Therefore, the angular velocity of the coil is
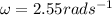 .
.