Answer:
Probability that from a sample of 200 Indianapolis residents, fewer than 170 were rooting for the Giants in Super Bowl XLVI is 0.02385.
Explanation:
We are given that Due to a decade-long rivalry between the Patriots and the city's own team, the Colts, most Indianapolis residents were rooting heartily for the Giants. Suppose that 90% of Indianapolis residents wanted the Giants to beat the Patriots.
Let p = % of Indianapolis residents wanted the Giants to beat the Patriots = 90%
The z-score probability distribution for proportion is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = % of Indianapolis residents who were rooting for the Giants in Super Bowl XLVI in a sample of 200 residents =
= % of Indianapolis residents who were rooting for the Giants in Super Bowl XLVI in a sample of 200 residents =
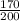 = 0.85
= 0.85
n = sample of residents = 200
So, probability that from a sample of 200 Indianapolis residents, fewer than 170 were rooting for the Giants in Super Bowl XLVI is given by = P(
 < 0.85)
< 0.85)
P(
 < 0.85) = P(
< 0.85) = P(
 <
<
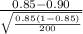 ) = P(Z < -1.98) = 1 - P(Z
) = P(Z < -1.98) = 1 - P(Z
 1.98)
1.98)
= 1 - 0.97615 = 0.02385
The above probability is calculated using z table by looking at value of x = 01.98 in the z table which have an area of 0.97615.
Therefore, probability that fewer than 170 were rooting for the Giants in Super Bowl XLVI is 0.02385.