Question

A model for​ consumers' response to advertising is given by the equation N(a)=2100+470ln(a) Where​ N(a) is the number of units​ sold, a is the amount spent on​ advertising, in thousands of​ dollars, & a≥1.

Answer 1

(a)5347 Units

(b)
`N^(')(a) =(470)/(a)`

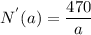
(c)The maximum point of N(a)=470. The minimum point does not exist.

Explanation:

a) How many units were sold after spending $1,000 on advertising?

N(a)=2100+470ln(a)

N(1000)=2100+470ln(1000)

=2100+3246.6

=5346.6 ≈ 5347 Units

b) We are required to find the derivative of N(a)

N(a)=2100+470ln(a)

`(d)/(da)N(a) = (d)/(da)(2100+470ln(a))\\N^(')(a) =(470)/(a)`

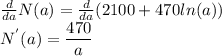
c) Find the maximum and minimum values of N(a) if they exist.

The maximum and/or minimum value of N(a) is the point at which the slope or derivative of N(a)=0.

Given that

`N^(')(a) =(470)/(a)=0\\N^(')(a) =470`

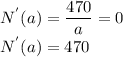
The maximum point of N(a)=470. The minimum point does not exist.