Question

Consider a circular dart board with radius one. I throw a dart at the board and record the (X,Y) position (note that the dart will land in the board, and (X,Y) are uniformly distributed on the board). 1. Find the marginal distribution of X

Answer 1

`f_X (x) = \frac{2\sqrt[]{1-x^2}}{\pi}`

Explanation:

Let R be the region the dart board. Hence, the region is described by the following inequality[/tex] R=\{(x,y): x^2+y^2 \leq 1\}[/tex]. We want to find the joint density function for (X,Y). We are given that this points are uniformly distributed, hence, the joint function is related to the area of the region. Hence,

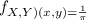`f_{X,Y)(x,y) = (1)/(\pi)`. Note that this function integrates up to one on the region R.

. (The area of R is pi given that it is a circle of radius 1.

Recall that the marginal distribution of X has the following pdf

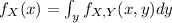`f_X (x) = \int_(y) f_(X,Y)(x,y) dy`. That is, fixing one value of x an integrating over the whole range of the variable Y.

Let
`w= \sqrt[]{1-x^2}`. Then, this w represents the value of y on the boundaries of the region R. Then,

`f_X (x) = \int_(-w)^(w) (1)/(\pi) dy = (2w)/(\pi) = \frac{2\sqrt[]{1-x^2}}{\pi}`. This is because, when we fix a value of X, we are integrating over a vertical line in the board, so Y goes from the bottom boundary of the circle and the upper boundary of the circle, whose points are described by our variable w.