Answer:
An 99% confidence interval of the given proportion
(0.355 , 0.385)
Explanation:
Given sample size n= 900
the number of successes in the sample is x=333
The proportion P =
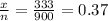
Q = 1-P =1 - 0.37 = 0.63
Confidence interval:-
99% of confidence interval zα = 2.93
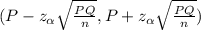
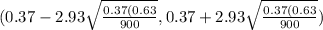
(0.37 - 0.015 , 0.37 + 0.015)
(0.355 , 0.385)
Conclusion:-
An 99% Confidence interval (0.355 , 0.385)