Question

Construct the 99% confidence interval estimate of the population proportion p if the sample size is n=900 and the number of successes in the sample is x=333. Use the Agrest-Coull method.

Answer 1

An 99% confidence interval of the given proportion

(0.355 , 0.385)

Explanation:

Given sample size n= 900

the number of successes in the sample is x=333

The proportion P =
`(x)/(n) = (333)/(900) = 0.37`

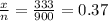
Q = 1-P =1 - 0.37 = 0.63

Confidence interval:-

99% of confidence interval zα = 2.93

`(P - z_(\alpha ) \sqrt{(PQ)/(n) } , P + z_(\alpha ) \sqrt{(PQ)/(n) })`

`(0.37 - 2.93 \sqrt{(0.37(0.63)/(900) } ,0.37 +2.93 \sqrt{(0.37(0.63)/(900) } })`

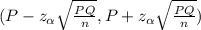
(0.37 - 0.015 , 0.37 + 0.015)

(0.355 , 0.385)

Conclusion:-

An 99% Confidence interval (0.355 , 0.385)