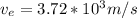Answer:
a
The orbital speed is

b
The escape velocity of the rocket is
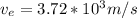
Step-by-step explanation:
Generally angular velocity is mathematically represented as
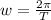
Where T is the period which is given as 1.6 days =
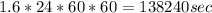
Substituting the value
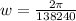
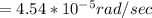
At the point when the rocket is on a circular orbit
The gravitational force = centripetal force and this can be mathematically represented as
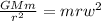
Where G is the universal gravitational constant with a value
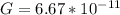
M is the mass of the earth with a constant value of
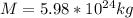
r is the distance between earth and circular orbit where the rocke is found
Making r the subject
![r = \sqrt[3]{(GM)/(w^2) }](https://img.qammunity.org/2021/formulas/physics/college/ayuxwvx1chh6bge2oebyul74lmi6g9uz0d.png)
![= \sqrt[3]{(6.67*10^(-11) * 5.98*10^(24))/((4.45*10^(-5))^2) }](https://img.qammunity.org/2021/formulas/physics/college/vj7f0hjzojf9zygoq8e3scpj7tynntqe33.png)
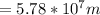
The orbital speed is represented mathematically as

Substituting value
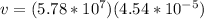

The escape velocity is mathematically represented as
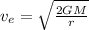
Substituting values