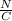Answer:
The induced electric field is 5.04
Step-by-step explanation:
Given:
Magnetic field
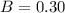 T
T
No. of turns
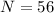
Radius of coil
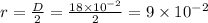
Change in time
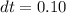 sec
sec
The magnetic magnetic field is give by,
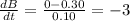
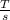
Here flux linked with the coil is,
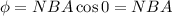
Using maxwell's equation,
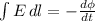
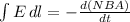
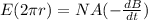
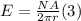
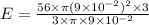
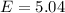
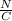
Therefore, the induced electric field is 5.04