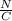Question

Calculate the induced electric field (in V/m) in a 56-turn coil with a diameter of 18 cm that is placed in a spatially uniform magnetic field of magnitude 0.30 T so that the face of the coil and the magnetic field are perpendicular. This magnetic field is reduced to zero in 0.10 seconds. Assume that the magnetic field is cylindrically symmetric with respect to the central axis of the coil. (Enter the magnitude.)

Answer 1

The induced electric field is 5.04
`(N)/(C)`

Step-by-step explanation:

Given:

Magnetic field
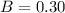`B = 0.30` T

No. of turns
`N = 56`

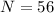
Radius of coil
`r = (D)/(2) = (18 * 10^(-2) )/(2) = 9 * 10^(-2)`

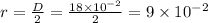
Change in time
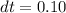`dt = 0.10` sec

The magnetic magnetic field is give by,

`(dB)/(dt) = (0-0.30)/(0.10) = -3`
`(T)/(s)`

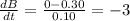
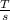
Here flux linked with the coil is,

`\phi = NBA\cos 0 = NBA`

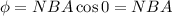
Using maxwell's equation,

`\int\limits {E} \, dl =- (d\phi)/(dt)`

`\int\limits {E} \, dl =- (d(NBA))/(dt)`

`{E} \((2\pi r) =NA(- (dB)/(dt))`

`E = (NA)/(2\pi r) (3)`

`E = (56 * \pi(9 * 10^(-2) )^(2) * 3 )/(3 * \pi * 9 * 10^(-2) )`

`E = 5.04`
`(N)/(C)`

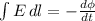
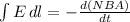
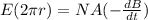
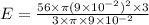
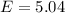
Therefore, the induced electric field is 5.04
`(N)/(C)`