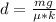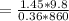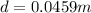Question

A 1.45-kg block is pushed against a vertical wall by means of a spring (k = 860 N/m). The coefficient of static friction between the block and the wall is 0.36. What is the minimum compression in the spring to prevent the block from slipping down? g

Answer 1

The minimum compression in the spring is
`d=0.0459m`

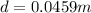
Step-by-step explanation:

From the question we are told that

The mass of the block is
`m_b = 1.45kg`

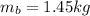
The spring constant is
`k =860 N/m`

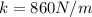
The coefficient of static friction is
`\mu = 0.36`

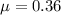
The mathematical relationship between the wight of the block and the force exerted by the spring is

`W_b = F_s`

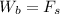
Where
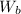`W_b` is mathematical represented as
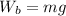`W_b = mg` and

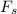`F_s` is mathematically represented as
`F_s = \mu * k *d`

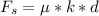
Where d is minimum length of compression in the spring to prevent the block from slipping

Now the relation can be wrtten as

`mg = \mu *k * d`

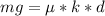
making d the subject we have

`d = (mg)/(\mu * k)`

`= (1.45* 9.8 )/(0.36 *860)`

`d=0.0459m`