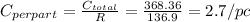Question

15. A cold-chamber die-casting machine operates automatically, supported by two industrial robots.The machine produces two zinc castings per cycle. One robot ladles molten metal into the chamber each cycle, and the other unloads the two castings from the machine and sprays lubricant onto the die cavities. Cycle time = 0.85 min. Each casting weighs 0.75 lbm, and the gating system weighs 0.40 lbm. The gating system can be recycled to cast more parts. Die cost = $45,000. The total production run = 200,000 pc. Scrap rate = 3%. Assume reliability = 100%. Cost of zinc = $1.05/lbm. Melting temperature of zinc = 787F. Its density = 0.258 lbm/in3 , heat of fusion = 49 Btu/lbm, and specific heat = 0.091 Btu/lbmF (use the same values of density and specific heat for solid and molten zinc). Pouring temperature = 860F. Heat losses account for 35% of the energy used to heat the metal. Cost of power for heating = $0.15/kWh. The cost rate of the die casting machine = $57/hr, and the cost rate of each robot = $18/hr. As part of the operation sequence, the casting is trimmed from the gating system, which is done manually at a labor rate of $20.00/hr. The worker recycles the zinc from the gating system for remelting. Determine (a) unit energy for melting and pouring, (b) total cost per hour to operate the cell, and (c) cost per part

Answer 1

a. 121 Btu/lb

b. 211.8lb

c. 2.69/pc

Step-by-step explanation:

See the attachments please

Answer 2

a) The unit energy for melting and pouring is 121 Btu/lb

b) The total cost per hour is 368.31/h

c) The cost per part is 2.7/pc

Step-by-step explanation:

a) The unit energy for melting and pouring is:

`U=C_(p) (T_(m,Zn) -T_(0) )+deltaH_(fus)+C_(p) (T_(p)- T_(0))`

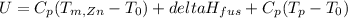
If we assume that the surrounding temperature is 70°F

`U=0.091(787-70)+49+0.091(860-787)=121Btu/lb`

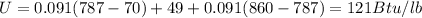
b) The hourly production is:

`R=((number-of-castings)/(t_(cycle) ) )*(1-scrap-rate)\\R=((2)/(0.85min) *(60min)/(1h) )*(1-0.03)=136.9good-parts/h`

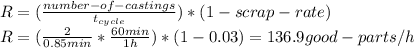
The total weight of zinc is:

`W_(total) =((number-of-castings)/(t_(cycle) ) )*(2*weight-of-casting)\\R=((2)/(0.85min) *(60min)/(1h) )*(2*0.75)=211.8lb`

The total cost of zinc is:

`C=W_(total) *cost-of-zinc=211.8*1.05=222.3` $

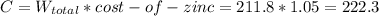The total heat transfer is:

`Q=((number-of-castings)/(t_(cycle) ) )*((2*weight-of-casting)+gating-system-weight)*U\\Q=((2)/(0.85min) *(60min)/(1h) )*((2*0.75)+0.4))*121=32462Btu/h=541Btu/min`

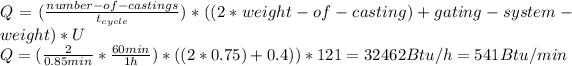
541 Btu/min = 9.51 kW

The power is:

`Power=(Q)/(1-Q_(loss) ) =(9.51)/(1-0.35) =14.6kW`

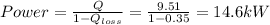
The hourly cost is:

`C_(H) =P*cost-of-power-for-heating=14.6*0.15=2.2/h`

The cost for die casting is:

`C_(d) =cost-rate-of-die-casting+(2*cost-of-each-robot)=57+(2*18)=93/h`

The die cost per casting is:

`C_(die,casting) =(45000)/(200000) =0.225/pc`

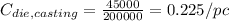
The hourly rate is:

`Hourly-rate=R*C_(d,casting) =136.9*0.225=30.81/h`

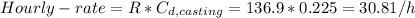
The total cost per hour is:

`C_(total) =C+C_(H) +C_(d) +C_(1) +Hourly-time=222.35+2.2+93+20+30.81=368.31/h`

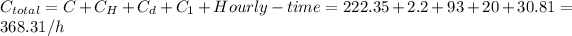
c) The cost per part is:

`C_(per part) =(C_(total) )/(R) =(368.36)/(136.9) =2.7/pc`