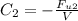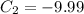Question

Assume that there are two jumpers. Assume that the first jumper is 85 kg and that the second jumper is 60 kg. Calculate the drag coefficients for each of these jumpers if they must both have the same velocity of 20 m/s in 6 seconds after jumping. Both jumpers are at rest initially and both jump from the same level (elevation).

Answer 1

To solve this problem we will apply the concepts related to the bearing and drag force. We will define the acceleration which will help us to find the force through the kinematic equations of linear motion. Subsequently, with said force equivalent to the drag force, we will calculate, by definition, the drag coefficient. Our values are defined as,

`\text{Mass of first jumper} = 85kg = m_1`

`\text{Mass of second jumper} = 60kg = m_2`

`Velocity = 20m/s`

`Time = t = 6s`

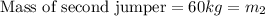
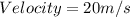
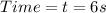
Now using equation,

`v = v_0 +at`

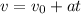
Where,

`v_0` = 0, Initial velocity

Acceleration

`a = (v)/(t)`

`a = (20)/(6)`

`a = 3.33m/s^2`

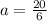
Now given relation is,

`F_u = -c'v`

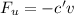
For first jumper

`F_(u1) =m_1a`

`F_(u1) = (85)(3.33)`

`F_(u1) = 283.05N`

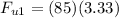
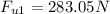
For second jumper

`F_(u2) = m_2a`

`F_(u2) = (60)(3.33)`

`F_(u2) = 199.8N`

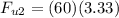
1) Drag coefficient for first jumper

`C_1 = -(F_(u1))/(V)`

`C_1 = -(283.05)/(20)`

`C_1 = -14.1525`

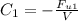
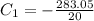
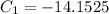
2) Drag coefficient for second jumper

`C_2 = -(F_(u2))/(V)`

`C_2 = -(199.8)/(20)`

`C_2 = -9.99`