Question

(5 points) The Daily Show. A 2010 Pew Research foundation poll indicates that among 1,099 college graduates, 33% watch The Daily Show. Meanwhile, of the 1,110 people in the poll with a high school degree but no college degree, 22% watch The Daily Show. A 95% confidence interval for pCollegeGrad−pHighSchoolpCollegeGrad−pHighSchool, where pp is the proportion of those who watch The Daily Show, is (0.07, 0.15). Based on this information, determine if the following statements are true or false, and explain your reasoning if you identify the statement as false.

1. There is a 95% chance that pCollegeGrad−pHighSchoolpCollegeGrad−pHighSchool is between 0.07 and 0.15. ? True False

2. We are 95% confident that 7% less to 15% more college graduates watch The Daily Show than those with a high school degree or less. ? True False

3. 95% of random samples of 1,099 college graduates and 1,110 people with a high school degree or less will yield differences in sample proportions between 7% and 15%. ? True False

4. 90% confidence interval for pCollegeGrad−pHighSchoolpCollegeGrad−pHighSchool would be wider. ? True False

5. A 95% confidence interval for pHighSchool−pCollegeGradpHighSchool−pCollegeGrad is (-0.15,-0.07). ? True False

Answer 1

(1) The statement is True.

(2) The statement is True.

(3) The statement is False.

(4) The statement is False.

(5) The statement is False.

Explanation:

The (1 - α)% confidence interval for population parameter implies that there is a (1 - α) probability that the true value of the parameter is included in the interval.

Or, the (1 - α)% confidence interval for the parameter implies that there is (1 - α)% confidence or certainty that the true parameter value is contained in the interval.

The 95% confidence interval for the difference between the proportion of college graduates and high school graduates who watch The Daily Show is (0.07, 0.15).

(1)

The statement is:

"There is a 95% chance that the difference between the proportion of college and high school graduates who watch The Daily show is between 0.07 and 0.15."

This statement is True.

This is because the 95% confidence interval for the difference between two proportions implies that there is 95% probability that the true difference between the proportions lies between 0.07 and 0.15.

(2)

The sample statistic is:

`\hat p_(college)-\hat p_(high\ school)`

So if the confidence interval consists of positive value it will imply that college graduates watch more of the Daily show.

The 95% confidence interval for the difference between two proportions implies that 7% less to 15% more college graduates watch The Daily Show than those with a high school degree or less.

Thus, the statement is True.

(3)

The 95% confidence interval (0.07, 0.15) estimates the value of the population proportion.

So the interval (0.07, 0.15) implies that if 100 such samples are selected and each sample is used to construct a 95% confidence interval then 95 of these confidence interval will consist the true difference value.

Thus, the statement is False.

(4)

The width of a confidence interval is:

`Width=z_(\alpha/2) * \sqrt{(\hat p(1-\hat p))/(n)}`

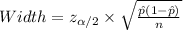
The width of the interval is directly proportional to the critical value.

The critical value of z increases as the confidence level increases an vice-versa.

So a 90% confidence level has a lower critical vale than the 95% confidence level.

Hence a 90% confidence interval will be narrower than the 95% confidence interval.

Thus, the statement is False.

(5)

The proportion of a random variable X lies in the range 0 to 1.

They do not assume negative values.

So the confidence interval for proportions cannot be negative.

Thus, the statement is False.