Final answer:
To solve the given differential equation dy/dt = -1/50(y - 17) for the temperature of the coffee at time t, we can use the method of separation of variables. The expression for the temperature of the coffee at time t is y = A
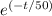 + 17.
+ 17.
Step-by-step explanation:
To solve the given differential equation dy/dt = -1/50(y - 17), we can use the method of separation of variables. Let's start by rearranging the equation:
dy/(y - 17) = -dt/50
Now, integrate both sides of the equation:
∫(dy/(y - 17)) = ∫(-dt/50)
ln|y - 17| = (-t/50) + C, where C is the constant of integration.
Next, solve for y by applying the natural logarithm property:
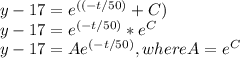
Finally, solve for y to obtain the expression for the temperature of the coffee at time t:
y = A
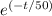 + 17
+ 17