Answer:
The expected number of checks among 784 that should have a leading digit of "1" is 236.
Explanation:
Let X = number of checks that has the leading digit as "1".
The probability of a check having a leading digit as "1" is, p = 0.301.
The number of checks issued by a suspected company is, n = 784.
A check is having a leading digit "1" is independent of other checks.
A randomly selected check either has the leading digit 1 or not.
The success of the experiment is defined as, a check having the digit "1" as the leading digit.
The random variable X follows a Binomial distribution with parameters n = 784 and p = 0.301.
The expected value of a random variable is the average number of times the random variable occurs.
The formula to compute the expected value of a Binomial distribution is:

Compute the expected value of X as follows:
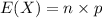
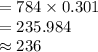
Thus, the expected number of checks among 784 that should have a leading digit of "1" is 236.