Question

The Brooklyn District Attorney's office analyzed the leading (leftmost) digits of check amounts in order to identify fraud. The leading digit of 1 is expected to occur 30.1% of the time, according to "Benford's law," which applies in this case. Among 784 checks issued by a suspect company, there were none with amounts that had a leading digit of 1. If there is a 30.1% chance that the leading digit of the check amount is 1, what is the expected number of checks among 784 that should have a leading digit of 1

Answer 1

The expected number of checks among 784 that should have a leading digit of "1" is 236.

Explanation:

Let X = number of checks that has the leading digit as "1".

The probability of a check having a leading digit as "1" is, p = 0.301.

The number of checks issued by a suspected company is, n = 784.

A check is having a leading digit "1" is independent of other checks.

A randomly selected check either has the leading digit 1 or not.

The success of the experiment is defined as, a check having the digit "1" as the leading digit.

The random variable X follows a Binomial distribution with parameters n = 784 and p = 0.301.

The expected value of a random variable is the average number of times the random variable occurs.

The formula to compute the expected value of a Binomial distribution is:

`E(X)=n* p`

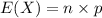
Compute the expected value of X as follows:

`E(X)=n* p\\`

`=784* 0.301\\=235.984\\\approx236`

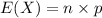
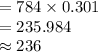
Thus, the expected number of checks among 784 that should have a leading digit of "1" is 236.