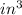Question

Find the dimensions of the open rectangular box of maximum volume that can be made from a sheet of cardboard 23 in. by 13 in. by cutting congruent squares from the corners and folding up the sides. Then find the volume. The dimensions of box of maximum volume are 17.66 comma 7.66 in.

Answer 1

The dimension of the box is 17.66 in by 7.66 in by 2.67 in.

Therefore the volume of the box is 361.19
`in^3`.

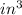Explanation:

Given that the dimensions of a cardboard is 23 in by 13 in.

Let the side of the square be x in.

Then the length of the box= (23-2x) in

and the width of the box =(13-2x) in

and height = x in.

The volume of the box is = length ×width × height

=[(23-2x)(13-2x)x]
`in^3`

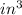
=(299x-72x² +4
`x^3`)
`in^3`

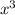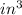
∴V=299x-72x² +4x³

Differentiating with respect x

V'= 299-144x+12x²

Again differentiating with respect x

V''= -144+24x

To find the dimensions, we set V'=0

∴299-144x+12x²=0

Applying Sridharacharya formula that is the solution of a quadratic equation ax²+bx+c is
`x=(-b\pm√(b^2-4ac))/(2a)`

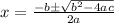
Here a=12, b=-144 , c=299

`\therefore x=(-(-144)\pm√((-144)^2-4.12.299))/(2.12)`

`\Rightarrow x= 9.33, 2.67`

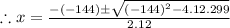
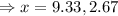
If we take x=9.33 in, then the width of the box [13-(2×9.33)] will negative.

∴x = 2.67 in

If at x = 2.67, V''<0 , then the volume of the box will be maximum or V''>0 then volume of the box will be minimum.

`V''|_(x=2.67)=-144+(24* 2.67)=-79.92<0`

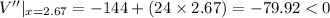
Therefore at x = 2.67, the volume of the box maximum.

The length of the box =[23-(2×2.67)] in

=17.66 in

The width of the box =[13-(2×2.67)] in

=7.66 in

The height of the box= 2.67 in

The dimension of the box is 17.66 in by 7.66 in by 2.67 in.

Therefore the volume of the box is =(17.66×7.66×2.67)
`in^3`

=361.19
`in^3`