Answer:
The dimension of the box is 17.66 in by 7.66 in by 2.67 in.
Therefore the volume of the box is 361.19
 .
.
Explanation:
Given that the dimensions of a cardboard is 23 in by 13 in.
Let the side of the square be x in.
Then the length of the box= (23-2x) in
and the width of the box =(13-2x) in
and height = x in.
The volume of the box is = length ×width × height
=[(23-2x)(13-2x)x]

=(299x-72x² +4
 )
)

∴V=299x-72x² +4x³
Differentiating with respect x
V'= 299-144x+12x²
Again differentiating with respect x
V''= -144+24x
To find the dimensions, we set V'=0
∴299-144x+12x²=0
Applying Sridharacharya formula that is the solution of a quadratic equation ax²+bx+c is
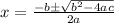
Here a=12, b=-144 , c=299

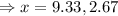
If we take x=9.33 in, then the width of the box [13-(2×9.33)] will negative.
∴x = 2.67 in
If at x = 2.67, V''<0 , then the volume of the box will be maximum or V''>0 then volume of the box will be minimum.
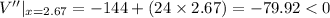
Therefore at x = 2.67, the volume of the box maximum.
The length of the box =[23-(2×2.67)] in
=17.66 in
The width of the box =[13-(2×2.67)] in
=7.66 in
The height of the box= 2.67 in
The dimension of the box is 17.66 in by 7.66 in by 2.67 in.
Therefore the volume of the box is =(17.66×7.66×2.67)

=361.19
