Question

A rectangular beam made of ABS plastic ( ) is b=20mm deep and t=10mm thick. Loads in the plane of the 20mm depth cause a bending moment of . What is the largest throughthickness edge crack that can be permitted if a safety factor of 2.5 against brittle fracture is required? (You may use .) (20points)

Answer 1

Here is the full question

A rectangular beam made of ABS plastic ( ) has dimensions b = 20 mm deep and t = 10 mm thick. Loads in the plane of the 20mm depth cause a bending moment of 10 N.m. What is the largest through thickness edge crack that can be permitted if a factor of safety of 2.5 against fracture is required?

Answer:

1.62 mm

Step-by-step explanation:

The formula for the stress intensity factor (K) for various bending, curves and equation label is expressed as:

`K = 1.12 S_g √(\pi a)`

where
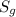`S_g` = gross section nominal stress for center cracked plate of ABS plastic rectangular beam and it's given as:

`S_g =(6 M)/(b^2 \ t)`

`S_g = (6(10 \ N.m))/((20 mm ( (1m)/(1,000mm))^2(10mm)((1m)/(1000mm)) )`

`S_g = 15*10^6N/m^2`

`S_g = 15MPa`

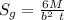
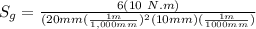
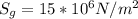
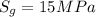
To determine the stress intensity factor K ; we have:

K =
`(K_(IC))/(X_K)`

From the table of fracture toughness of polymers and ceramics at room temperature, we selected the fracture toughness of ABS plastics material to be :

`3MPa √(m)`

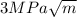
So; K =
`(3MPa √(m))/(2.5)`

`= 1.2 MPa √(m)`

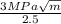
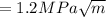
The largest through thickness edge crack that can be permitted due to bending moment of 10 N.m is :

`1.12(15MPa)√(\pi a) = 1.2 MPa √(m)`

a =
`(0.0051)/(3.14)`

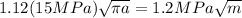
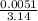
a = 0.00162 m

a = 1.62 mm

Thus , the largest through thickness edge crack that can be permitted due to bending moment of 10 N.m is 1.62 mm