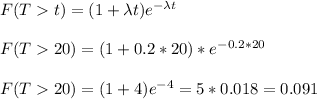Question

Suppose a phone call on average lasts 5 minutes at a phone booth.(a) If a person arrives at a public telephone booth just before you, calculate the probability that youhave to wait more than 15 minutes to make your call. (Hint: Use exponential distribution to modelwaiting time)(b) You get tired of waiting, and decide to do a little shopping and come back. When you come backthere are now 2 people ahead of you. What is the probability that that you have to wait more than20 minutes?

Answer 1

a) The probability that the call last more than 15 minutes is P(T>15)=0.050.

b) The probability that that you have to wait more than 20 minutes is P(T>20)=0.091.

Explanation:

The call time is exponentially distributed with a mean of 5 minutes.

The parameter of the exponential distribution is:

`\lambda=(1)/(Mean) =1/5=0.2`

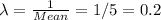
a) The probability that the call last more than 15 minutes is:

`F(T>t)=e^(-\lambda\cdot t)\\\\F(T>15)=e^(-0.2*15)=e^(-3)=0.050`

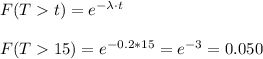
b) Now we have to work with the sum of two independent exponential variables with the same parameter.

The probability that the two calls last more than 20 minutes can be written as:

`F(T>t)=(1+\lambda t)e^(-\lambda t)\\\\F(T>20)=(1+0.2*20)*e^(-0.2*20)\\\\F(T>20)=(1+4)e^(-4)=5*0.018=0.091`