Answer:
It is proved that
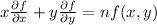 .
.
Explanation:
Given function is,
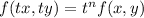 for all t>0 and n is positive integers.
for all t>0 and n is positive integers.
To show,

Let, u=tx and v=ty, then,
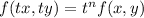

differentiate partially with respect to x we get,
[tex}\frac{\partial}{\partial x}f(u,v)=\frac{\partial}{\partial x}(t^nf(x, y))[/tex]
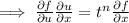
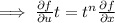
Again, differentiate (1) with respect to t we get,
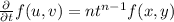
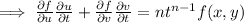

 (By putting values of
(By putting values of
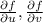 )
)
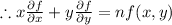
Hence proved.