Answer:
(a) velocity function: 3t² - 12
(b) acceleration function: 6t
(c) the particle is moving forward when t > 2
(d) the particle is moving backward when t < 2
(e) the particle travels -9 m
Step-by-step explanation:
position: s(t) = t³ − 12t + 3.
(a) by definition, velocity = ds/dt = 3t² - 12
(b) by definition, acceleration = d²s/dt² = 6t
(c) A particle moves forward when its velocity is positive. That is:
3t² - 12 > 0
3t² > 12
t² > 12/3
t² > 4
t > 2
(d) A particle moves backwards when its velocity is negative. That is:
3t² - 12 < 0
3t² < 12
t² < 12/3
t² < 4
t < 2
(e) The distance is computed as follows:
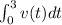
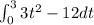
![3^3 - 12(3) - [ 0^3 - 12(0) ]](https://img.qammunity.org/2021/formulas/physics/high-school/1548tvhhl54mch065svkpvccl2au8ey6jt.png)
-9