Answer:
Correct option: (a) 0.1452
Explanation:
The new test designed for detecting TB is being analysed.
Denote the events as follows:
D = a person has the disease
X = the test is positive.
The information provided is:
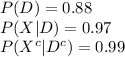
Compute the probability that a person does not have the disease as follows:
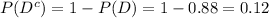
The probability of a person not having the disease is 0.12.
Compute the probability that a randomly selected person is tested negative but does have the disease as follows:
![P(X^(c)\cap D)=P(X^(c)|D)P(D)\\=[1-P(X|D)]* P(D)\\=[1-0.97]* 0.88\\=0.03* 0.88\\=0.0264](https://img.qammunity.org/2021/formulas/mathematics/college/76d6xnu7brfnxw65m5pvzmw835e6813sbi.png)
Compute the probability that a randomly selected person is tested negative but does not have the disease as follows:
![P(X^(c)\cap D^(c))=P(X^(c)|D^(c))P(D^(c))\\=[1-P(X|D)]*{1- P(D)]\\=0.99* 0.12\\=0.1188](https://img.qammunity.org/2021/formulas/mathematics/college/ypww5vt17vgnsfyxtqlcnw5wybffx948tm.png)
Compute the probability that a randomly selected person is tested negative as follows:
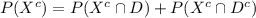
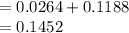
Thus, the probability of the test indicating that the person does not have the disease is 0.1452.