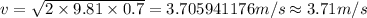Answer:
3.71 m/s
Step-by-step explanation:
From the law of conservation of linear momentum, since we are neglecting minor energy losses due to friction then we can express it as
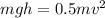 since all the potential energy is transformed to kinetic energy
since all the potential energy is transformed to kinetic energy
Making v the subject of the formula then
 and here m is the mass of the block, g is acceleration due to gravity, h is the height. Substituting 0.7 m for h and 9.81 for g then we obtain that
and here m is the mass of the block, g is acceleration due to gravity, h is the height. Substituting 0.7 m for h and 9.81 for g then we obtain that