Answer:
(a) Shown below
(b) The expected time it takes for the bus to arrive is 7.5 minutes.
(c) The probability that the bus was missed if I arrived at the bus stop at 9:07 AM is 0.40.
Explanation:
Let X = waiting time for the bus.
It is provided that the bus arrives at the bus stop uniformly between 9:05 AM and 9:10 AM.
The random variable X is uniformly distributed with parameters a = 5 and b = 10.
The probability density function of a Uniform distribution is:
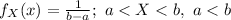
(a)
The probability density function of the random variable X is:
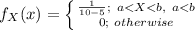
The cumulative distribution function of the random variable X is:
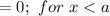
![F_(X)(x)=(x-a)/(b-a)=(x-5)/(10-5);\ x\epsilon[a, b]](https://img.qammunity.org/2021/formulas/mathematics/college/rlvepzhrgi8oz085k41mhx387e6i3749ze.png)
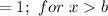
(b)
The expected value of Uniform distribution is:
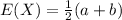
Compute the expected value of X as follows:
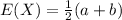
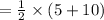
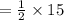
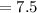
Thus, the expected time it takes for the bus to arrive is 7.5 minutes.
(c)
If I reach the bus stop at 9:07 AM and I have missed the bus, then this implies that the bus arrived between 9:05 AM and 9:07 AM.
Compute the probability that the bus arrived between 9:05 AM and 9:07 AM as follows:
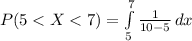
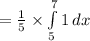

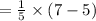
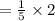
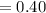
Thus, the probability that the bus was missed if I arrived at the bus stop at 9:07 AM is 0.40.