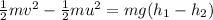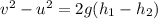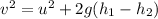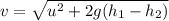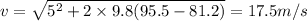Question

A 4,500-kg roller coaster cart has a speed of 5.00 m/sm/s when it reaches its first peak at a 95.5 mm height from the ground level. After descending, it climbs up the second hill which is 81.2 mm above the ground level. How fast is the roller coaster cart at the top of the second hill? Assume there is no friction with the rails and no air resistance during the cart's motion.

Answer 1

17.5 m/s

Step-by-step explanation:

We are given that

Mass ,m=4500 kg

Initial speed,u=5 m/s

`h_1=95.5 m`

`h_2=81.2 m`

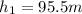
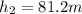
We have to find the speed of roller coaster cart at the top of the second hill.

According to law of conservation of energy

Change in kinetic energy=Change in potential energy

`(1)/(2)mv^2-(1)/(2)mu^2=mg(h_1-h_2)`

`v^2-u^2=2g(h_1-h_2)`

`v^2=u^2+2g(h_1-h_2)`

`v=√(u^2+2g(h_1-h_2))`

`v=√(5^2+2* 9.8(95.5-81.2))=17.5 m/s`