Question

A simple regression model is used to forecast sales with advertising expenditures. The regression output indicates that the coefficient of advertising expenditures is positive and statistically significant. The output also indicates that the correlation between sales and advertising expenditures is 0.9132. Based on these results, we can conclude that spending more on advertising causes sales to go up.

O True
O False

Answer 1

For this case the correlation coefficient calculated is r =0.9132

In order to test the hypothesis if the correlation coefficient it's significant we have the following hypothesis:

Null hypothesis:
`\rho =0`

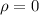
Alternative hypothesis:
`\rho \\eq 0`

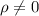
The statistic to check the hypothesis is given by:

`t=(r √(n-2))/(√(1-r^2))`

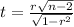
We don't know the sample size for this case but since we know that coefficient of advertising expenditures is positive and statistically significant and the correlation coeffcient is very high (near to 1) we can conclude that the relation is linear and proportional so the answer would be:

TRUE

Explanation:

Previous concepts

The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.

And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

Solution to the problem

For this case the correlation coefficient calculated is r =0.9132

In order to test the hypothesis if the correlation coefficient it's significant we have the following hypothesis:

Null hypothesis:
`\rho =0`

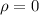
Alternative hypothesis:
`\rho \\eq 0`

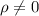
The statistic to check the hypothesis is given by:

`t=(r √(n-2))/(√(1-r^2))`

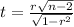
We don't know the sample size for this case but since we know that coefficient of advertising expenditures is positive and statistically significant and the correlation coeffcient is very high (near to 1) we can conclude that the relation is linear and proportional so the answer would be:

TRUE