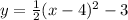Question

Find the equation, (f(x) = a(x - h)2 + k), for a parabola containing point (2, -1) and having (4, -3) as a vertex. What is the standard form of the equation?

Answer 1

Given that the vertex of the parabola is (4,-3)

The parabola passes through the point (2,-1)

We need to determine the standard form of the equation of the parabola.

Standard form of the equation of the parabola:

The standard form of the equation is
`y=a(x-h)^2+k` where the vertex is (h,k) and a is the constant.

Substituting the vertex (4,-3) in the above equation, we get;

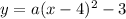`y=a(x-4)^2-3` ---------------(1)

Substituting the point (2,-1) in the above equation, we have;

`-1=a(2-4)^2-3`

`-1=a(-2)^2-3`

`-1=4a-3`

`2=4a`

`(1)/(2)=a`

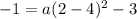
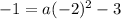
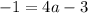
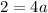
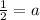
Thus, the value of a is
`(1)/(2)`

Substituting the value of a in the equation (1), we get;

`y=(1)/(2)(x-4)^2-3`

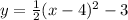
Thus, the standard form of the equation of the parabola is
`y=(1)/(2)(x-4)^2-3`