Answer:
Explanation:
7) Volume of the shape = Volume of triangular prism - volume of cylinder
Triangular prism:

b = 6 ft & height of the triangle = 5 ft
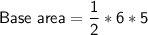
= 3*5
= 15 ft²
Volume of prism = 15 * 4
= 60 ft³
Cylinder:
r = 2÷2 = 1 ft & h = 4 ft
Volume of cylinder = 3.14 * 1 * 1 * 4
= 12.56 ft³
Volume of the shape = 60 - 12.56
= 47.44 ft³
8) Volume = Volume of Pyramid - Volume of cone
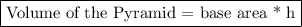
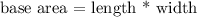
= 9 * 9
= 81 m²
Volume of Pyramid = 81 * 8
= 648 m³

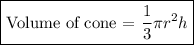
r = diameter ÷ 2 = 6÷2
r = 3 m & h = 8 m
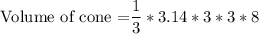
= 3.14 * 3 * 8
= 75.36 m³
Volume of the shape = 648 - 75.36
= 572.64 m³
9) Volume of the shape = volume of cylinder + volume of cone
Cylinder:
h = 7 in ; r = 3
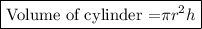
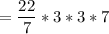
= 22 *3 * 3
= 198 in³
Cone:
r = 3 in & h = 4 in
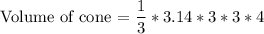
= 3.14 * 3 * 4
= 37.68 in³
Volume of the shape = 198 + 37.68
= 235.68 in³
10) Volume of the shape = Volume of outer cyliner - volume of inner cylinder
Volume of outer cylinder:
R = 9 m & h = 3 m
Volume of outer cylinder = 3.14 * 9 * 9 * 3
= 763.02 m³
Volume of inner cylinder:
r = 5 m & h = 3 m
Volume of inner cylinder = 3.14 * 5 * 5 * 3
= 235.5 m³
Volume of the shape = 763.02 - 235.5
= 527.52 m³