Answer:
c) -2y = 10x + 6
Explanation:
The equation of a line in slope-intercept form is:

The variables stand for:

Plugging in the given information into the equation:
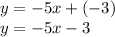
Go through the answer choices:
a) 2y = -5x - 3
Divide both sides of the equation by 2
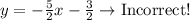
b) -2y = 10x - 6
Divide both sides of the equation by -2
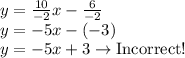
c) -2y = 10x + 6
Divide both sides of the equation by -2

d) 2y = 10x - 6
Divide both sides of the equation by 2
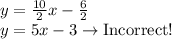
Therefore the answer is c) -2y = 10x + 6
Additional Comments:
We can only divide both sides of the equation by 2 and/or -2 because of the Division Property of Equality. This property states that if we divide one side of the equation by a certain quantity, we must divide the other side by the same quantity so that the equation remains equal.