Question

The graph shown represents the number of bacteria in a dish after a certain number of minutes. It is a function in the form f(x) = a · bx.

Answer 1

The number of bacteria in the dish after 9.9 minutes is 478

Explanation:

The form of the function is
`f(x)=a.b^(x)` , where a is the initial amount (value f(x) at x = 0)

To find a and b let us use two points from the graph and substitute their coordinates in the equation

∵ The graph passes through point (1 , 1)

∴ x = 1 and y = 1

- Substitute them in the equation

∵
`1=a.b^(1)`

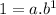
∴ a.b = 1 ⇒ (1)

∵ The graph passes through point (1 , 1)

∴ x = 3 and y = 4

- Substitute them in the equation

∵
`4=a.b^(3)`

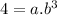
∴ a.b³ = 4 ⇒ (2)

Use equation (1) to find a in terms of b

∵ a.b = 1

- Divide both sides by b

∴
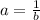`a=(1)/(b)` ⇒ (3)

- Substitute a in equation (2) by equation (3)

∴
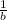`(1)/(b)` . b³ = 4

- Remember the rule
`(a^(m))/(a^(n))=a^(m-n)`

∵
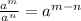
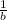`(1)/(b)` . b³ =
`b^(3-1)` = b²

∴ b² = 4

- Take √ for both sides

∴ b = 2

Substitute the value of b in equation (3) to find a

∵ a =
`(1)/(2)`

∴ a = 0.5

∴
`f(x)=0.5(2)^(x)`

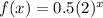
∵ f(x) represents the number of bacteria after x minutes

∵ x = 9.9 minutes

- Substitute x by 9.9 to find the number of bacteria

∵
`f(9.9)=0.5(2)^(9.9)`

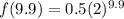
∴ f(9.9) = 477.7128917

- Round it to the nearest whole number

∴ f(9.9) = 478

∴ The number of bacteria in the dish after 9.9 minutes is 478