Question

The cross section of a water trough is shaped like a trapezoid. The bases of the trapezoid are 18 feet and 8 feet long. It has an area of 52 squared feet. What is the height of the cross section?

Answer 1

it's 94

Explanation:

i just took it

Answer 2

The height of the trapezoid cross section is H = 4 ft

Explanation:

From the figure

AB = 18 ft

CD = 8 ft

Area of the trapezoid = 52
`ft^(2)`

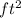
We know that area of the trapezoid is given by

A = 0.5 × ( AB + BC ) × Height of the trapezoid ------ (1)

Put all the values in above formula we get

52 = 0.5 × ( 18 + 8 ) × H

H = 4 ft

Therefore the height of the trapezoid cross section is H = 4 ft