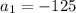Question

Recursive formula for this geometric sequence, -125, -25, -5, -1

Answer 1

`a_n= (1)/(5) \cdot a_(n-1) \\ a_n= - 125`

Explanation:

The given geometric sequence is:

-125, -25, -5, -1

We want to find a recursive formula for the given geometric sequence.

The first term of this sequence is

`a_1=-125`

The common ratio is

`r = ( - 1)/( - 5) = (1)/(5)`

The recursive definition is given by:

`a_n=r\cdot a_(n-1)`

We substitute the ratio to get:

`a_n= (1)/(5) \cdot a_(n-1) \\ a_n= - 125`

Answer 2

Recursive formula for this geometric sequence, -125, -25, -5, -1 will be:

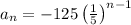`a_n=-125\left((1)/(5)\right)^(n-1)` where
`a_1=-125`

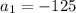
Explanation:

As we know that when we define a sequence by describing the relationship between its successive terms, it means we are defining the sequence recursively.

Given that,

-125, -25, -5, -1

`\mathrm{Compute\:the\:ratios\:of\:all\:the\:adjacent\:terms}:\quad \:r=(a_(n+1))/(a_n)`

`(-25)/(-125)=(1)/(5),\:\quad (-5)/(-25)=(1)/(5),\:\quad (-1)/(-5)=(1)/(5)`

`\mathrm{The\:ratio\:of\:all\:the\:adjacent\:terms\:is\:the\:same\:and\:equal\:to}`

`r=(1)/(5)`

`\mathrm{The\:first\:element\:of\:the\:sequence\:is}`

`a_1=-125`

`a_n=a_1\cdot r^(n-1)`

`\mathrm{Therefore,\:the\:}n\mathrm{th\:term\:is\:computed\:by}\:`

`a_n=-125\left((1)/(5)\right)^(n-1)`

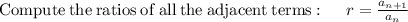
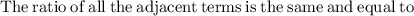
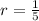
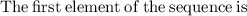
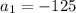
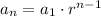
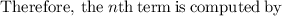
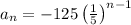
As the recursive formula makes us able to find the next term in the sequence from the proceeding term by multiplying the preceding term by r.

Therefore,

Recursive formula for this geometric sequence, -125, -25, -5, -1 will be:

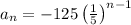`a_n=-125\left((1)/(5)\right)^(n-1)` where
`a_1=-125`