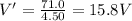Answer:
15.8 V
Step-by-step explanation:
The relationship between capacitance and potential difference across a capacitor is:
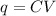
where
q is the charge stored on the capacitor
C is the capacitance
V is the potential difference
Here we call C and V the initial capacitance and potential difference across the capacitor, so that the initial charge stored is q.
Later, a dielectric material is inserted between the two plates, so the capacitance changes according to

where k is the dielectric constant of the material. As a result, the potential difference will change (V'). Since the charge stored by the capacitor remains constant,
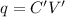
So we can combine the two equations:

and since we have
V = 71.0 V
k = 4.50
We find the new potential difference: